数据类型
数据对象
- 数据对象又称为样本、实例、数据点、对象或元组
- 数据对象用属性描述
- 数据表的行对应数据对象;列对应属性
- 一个数据对象代表一个实体
销售数据库:顾客、商品、销售记录
医疗数据库:患者、医生、诊断治疗记录
大学数据库:学生、教授、课程
数据属性
- 属性也称为特征(机器学习)、维度(数据库)、变量(统计学)
- 属性是一个数据字段,表示数据对象的一个特征。数据对象的所有属性称为属性向量,或特征向量。
- 属性类型:
标称属性、二元属性、序数属性、数值属性
标称属性:对象的标号、类别、编码或者状态等可列举值
- 值不必具有次序信息,类似于编程语言中的枚举类型。
- 头发颜色={黑色,金色,棕色,褐色,白色,灰色}
- 职业、邮政编码等
二元属性也称为布尔属性
也是一种标称属性,只有两个状态:0或者1
对称的(symmetric):两种状态具有同等价值
- 如:性别
非对称的(asymmetric):状态的权重不一样
- 如:体检报告(阴性和阳性)
- 惯例:重要的结果使用编码1(如,流感病毒阳性)
序数属性的可能值之间具有有意义的序(ranking),但是相继值之间的差是未知的
- 咖啡:“小杯”、“中杯”和“大杯”
- 职称:讲师、副教授、教授
一般用于标识不能客观度量的主观性评价
- 如调查报告:对客服的满意度调查,0-很不满意;1-不太满意;2-基本满意;3-满意;4-非常满意
数值属性是定量的,可观测的数值,用整数或者实数度量。
区间标度数值:
- 用相等的单位度量,有序,相继值的差值有意义,相继值的比率没有意义
- 如:温度,10度天气,5度天气,无法说热/冷2倍
比率标度数值:
- 用相等的单位度量,有序,相继值的差值、比率都有意义
- 如:体重、身高、速度等
离散属性 VS 连续属性
- 机器学习通常把属性分成两类:离散和连续
- 离散属性有有限的或者无限可数的值集合,可以用整数表示
- 如果值不是离散的,则是连续属性。数值属性和连续属性在含义上是一样的。
数据的基本统计描述
中心趋势度量
- 均值、中位数、众数、中列数
均值
均值是描述数据集常用的统计量,但容易受到极端值的影响。
解决方案:截尾均值:去除排序后高端和低端2%的值之后再计算
中位数
一组有序数据值的中间值
- 有一半的数比他小,另一半的数比他大
如果值有奇数个,取中间值;否则取中间两数的平均
- 例:数据按递增排序为:33,45,60,65,70,77,80,90,100,100。有10个观测值,因此中位数为中间两个值得平均值。中位数为:(70+77)/2=73.5
利用中位数(上)下限公式估计(分组数据)
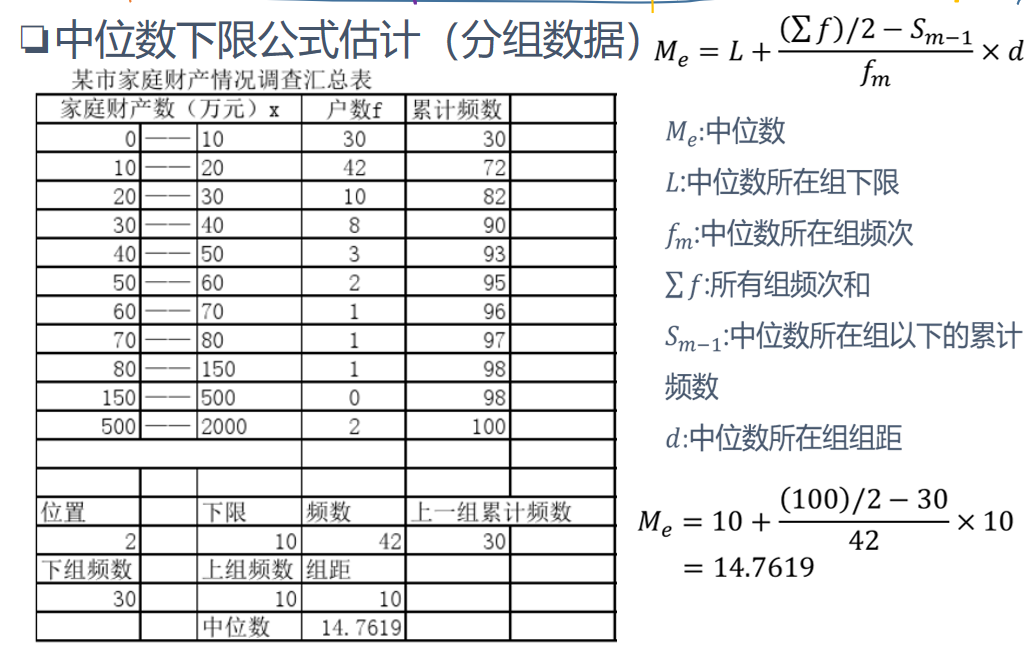
众数
数据中出现频率最高的值
- 例:数据按递增排序为:33,45,60,65,70,77,80,90,100,100。
- 则mode = 100。
当数据中有多个高频率数值时,会有多个众数。
当每个数据值仅出现一次,则没有众数。
经验公式: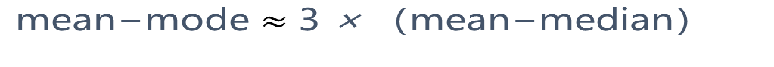
中列数
中列数是最大值和最小值的平均值。
- 例:数据按递增排序为:33,45,60,65,70,77,80,90,100,100。
- 则中列数 =(33+100)/ 2 = 66.5。
均值、中位数、众数区别
- 每个数据的变化,都会影响均值
- 中位数通过排序获得,不受最大、最小两端极值数值影响。部分数据的变动对中位数没有影响,当一组数据中的个别数据变动较大时,常用中位数描述这组数据的中心趋势。
- 众数也反映了一组数据的集中程度和频度。日常生活中诸如“最佳”、“最受欢迎”、“最满意”等,都与众数有关,通过频度反映了普遍的倾向性。
数据分散度量
- 极差、四分位数、四分位数极差、方差、标准差
极差
极差是数据中最大值和最小值的差值。
- 例:数据按递增排序为:33,45,60,65,70,77,80,90,100,100。
- 则range = 100-33=67。
分位数
分位数是取自数据分布的每隔一定间隔的点,把数据划分成基本大小相等的连贯集合
四分位数: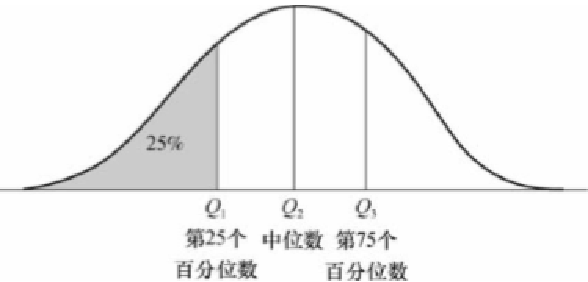
四分位数极差IQR: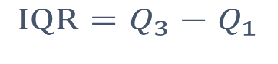
五数概括法:min,Q1,median,Q3,max
- min = Q1 - 1.5*IQR
- max = Q3 + 1.5*IQR
离群点:落在Q3之上或Q1之下至少1.5*IQR
方差与标准差
方差(方差,Variance,var):各个数据与平均数差值平方和的平均数。
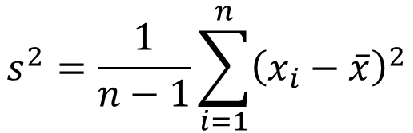
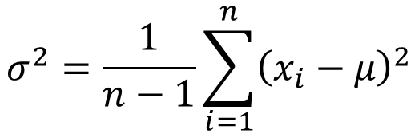
标准差(Standard Deviation,std):方差的平方根
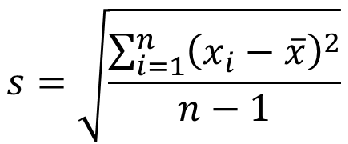
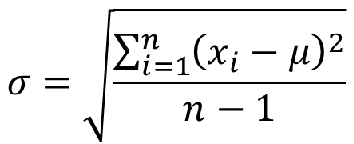
基本统计图
- 箱图、饼图、直方图、散点图
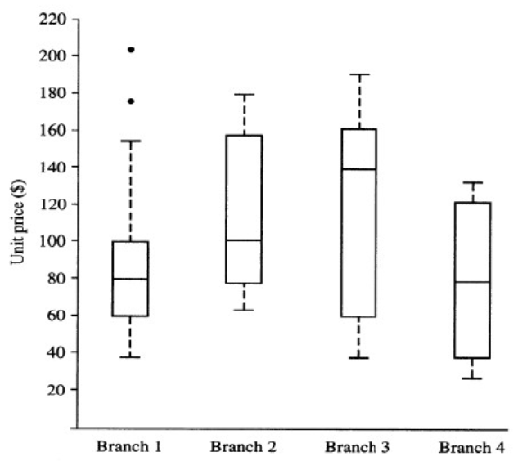
箱图
箱图反映五数概括:min,Q1,median,Q3,max
- 一组数据用一个箱子表示
- 箱子的长度是四分位极差
- 中间线是中值
- 箱子外面的两条线是观察的min和max
- 离群点:阈值范围外的点
直方图
直方图:又称为频率直方图、频率分布直方图,在统计学上表示频率分布的图形。
饼图
饼图用于显示每一个数占总数的比例
散点图
散点图是指在回归分析中,数据点在直角坐标系平面上的分布图。

