Apriori算法的简介

Apriori算法：使用候选项集找频繁项集

Apriori算法是一种最有影响的挖掘布尔关联规则频繁项集的算法。其核心是基于两阶段频集思想的递推算法。该关联规则在分类上属于单维、单层、布尔关联规则。在这里，所有支持度大于最小支持度的项集称为频繁项集，简称频集。

Apriori原理：如果某个项集是频繁的，那么它的所有子集也是频繁的。该定理的逆反定理为：如果某一个项集是非频繁的，那么它的所有超集（包含该集合的集合）也是非频繁的。Apriori原理的出现，可以在得知某些项集是非频繁之后，不需要计算该集合的超集，有效地避免项集数目的指数增长，从而在合理时间内计算出频繁项集。

支持度，置信度，提升度

支持度

表示同时购买X、Y的订单数占总订单数（研究关联规则的“长表”中的所有购买的产品的订单数）的比例。如果用P(X)表示购买X的订单比例，其他产品类推，那么

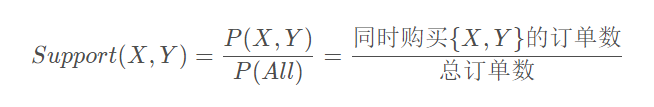
置信度

表示购买X的订单中同时购买Y的比例，即同时购买X和Y的订单数占购买X的订单的比例。公式表达：

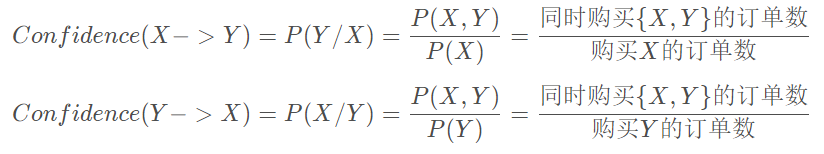
提升度

提升度反映了关联规则中的X重点内容与Y的相关性：提升度 >1 且越高表明正相关性越高;提升度 <1 且越低表明负相关性越高;提升度 =1 表明没有相关性。

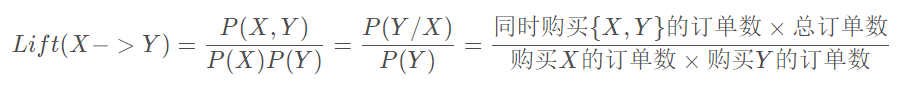
Apriori算法的编程实现

题目

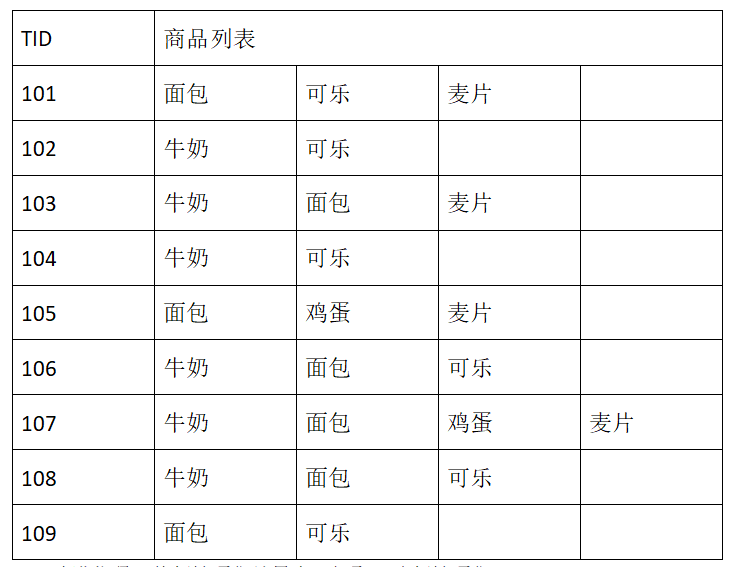
数据集

要求：

• 从频繁项集结果中，提取2阶频繁项集
• 使用seaborn工具包，实现2阶频繁项集的热力度表示
• 计算2阶频繁项集的置性度（Confidence）和提升度（Lift）。定义最小置性度阈值，并生成和输出2阶关联规则

代码

# by 陈良辉
import seaborn as sns
import pandas as pd

def loadDataSet():
    #return [['面包', '可乐', '麦片'], ['牛奶', '可乐'], ['牛奶','面包', '麦片'], ['牛奶', '可乐'], ['面包','鸡蛋', '麦片'], ['牛奶','面包', '可乐'], ['牛奶','面包','鸡蛋', '麦片'], ['牛奶','面包', '可乐'],['面包', '可乐']]
    return [[1, 2, 3], [4, 2], [4,1, 3], [4, 2], [1,5, 3], [4,1, 2], [4,1,5,3], [4,1, 2],[1,2]]

# 获取候选1项集，dataSet为事务集。返回一个list，每个元素都是set集合
def createC1(dataSet):
    C1 = []   # 元素个数为1的项集（非频繁项集，因为还没有同最小支持度比较）
    for transaction in dataSet:
        for item in transaction:
            if not [item] in C1:
                C1.append([item])
    C1.sort()  # 这里排序是为了，生成新的候选集时可以直接认为两个n项候选集前面的部分相同
    # 因为除了候选1项集外其他的候选n项集都是以二维列表的形式存在，所以要将候选1项集的每一个元素都转化为一个单独的集合。
    return list(map(frozenset, C1))   #map(frozenset, C1)的语义是将C1由Python列表转换为不变集合（frozenset，Python中的数据结构）

# 找出候选集中的频繁项集
# dataSet为全部数据集，Ck为大小为k（包含k个元素）的候选项集，minSupport为设定的最小支持度
def scanD(dataSet, Ck, minSupport):
    ssCnt = {}   # 记录每个候选项的个数
    for tid in dataSet:
        for can in Ck:
            if can.issubset(tid):
                ssCnt[can] = ssCnt.get(can, 0) + 1   # 计算每一个项集出现的频率
    numItems = float(len(dataSet))
    retList = []
    supportData = {}
    for key in ssCnt:
        support = ssCnt[key] / numItems
        if support >= minSupport:
            retList.insert(0, key)  #将频繁项集插入返回列表的首部
        supportData[key] = support
    return retList, supportData   #retList为在Ck中找出的频繁项集（支持度大于minSupport的），supportData记录各频繁项集的支持度

# 通过频繁项集列表Lk和项集个数k生成候选项集C(k+1)。
def aprioriGen(Lk, k):
    retList = []
    lenLk = len(Lk)
    for i in range(lenLk):
        for j in range(i + 1, lenLk):
            # 前k-1项相同时，才将两个集合合并，合并后才能生成k+1项
            L1 = list(Lk[i])[:k-2]; L2 = list(Lk[j])[:k-2]   # 取出两个集合的前k-1个元素
            L1.sort(); L2.sort()
            if L1 == L2:
                retList.append(Lk[i] | Lk[j])
    return retList

# 获取事务集中的所有的频繁项集
# Ck表示项数为k的候选项集，最初的C1通过createC1()函数生成。Lk表示项数为k的频繁项集，supK为其支持度，Lk和supK由scanD()函数通过Ck计算而来。
def apriori(dataSet, minSupport=0.5):
    C1 = createC1(dataSet)  # 从事务集中获取候选1项集
    D = list(map(set, dataSet))  # 将事务集的每个元素转化为集合
    L1, supportData = scanD(D, C1, minSupport)  # 获取频繁1项集和对应的支持度
    L = [L1]  # L用来存储所有的频繁项集
    k = 2
    while (len(L[k-2]) > 0): # 一直迭代到项集数目过大而在事务集中不存在这种n项集
        Ck = aprioriGen(L[k-2], k)   # 根据频繁项集生成新的候选项集。Ck表示项数为k的候选项集
        Lk, supK = scanD(D, Ck, minSupport)  # Lk表示项数为k的频繁项集，supK为其支持度
        L.append(Lk);supportData.update(supK)  # 添加新频繁项集和他们的支持度
        k += 1
    return L, supportData

def draw_seaborn(suppData,n):
    list1 = []
    list2 = []
    list3 = []
    for i in range(n):
        list4 = []
        list1.append(i+1)
        list2.append(i+1)
        for j in range(n):
            a = list(map(frozenset,[[i+1,j+1]]))[0]
            if a in suppData:
                list4.append(suppData[a])
            else:
                list4.append(0.00)
        list3.append(list4)
    data = {}
    for num in range(n):
        data[list1[num]] = list3[num]
    df = pd.DataFrame(data,index = list2,columns = list1) 
    return sns.heatmap(df, linewidths=.5,annot=True)

def data_deal(L,suppData):
    min = -1
    DataList = []
    for i in range(len(L[1])):
        for j in L[1][i]:
            if i > min:
                min = i
                List = []
                List.append(suppData[L[1][i]])
            List.append(j)
        DataList.append(List)
    Datanum = {}
    for m in range(len(L[0])):
        Datanum[len(L[0])-m] = L[0][m]
    return DataList, Datanum

def confidence(DataList, Datanum, suppData):
    confidence_data = {}
    for num in range(len(DataList)):
        str1 = ''
        str2 = ''
        str1 = str(DataList[num][1]) + '->' + str(DataList[num][2])
        confidence_data[str1] = DataList[num][0]/suppData[Datanum[DataList[num][1]]]
        str2 = str(DataList[num][2]) + '->' + str(DataList[num][1])
        confidence_data[str2] = DataList[num][0]/suppData[Datanum[DataList[num][2]]]
    return confidence_data

def Lift(DataList, confidence_data, Datanum, suppData):
    Lift_data = {}
    for num in range(len(DataList)):
        str1 = ''
        str2 = ''
        str1 = str(DataList[num][1]) + '->' + str(DataList[num][2])
        Lift_data[str1] = confidence_data[str1]/suppData[Datanum[DataList[num][2]]]
        str2 = str(DataList[num][2]) + '->' + str(DataList[num][1])        
        Lift_data[str2] = confidence_data[str2]/suppData[Datanum[DataList[num][1]]]
    return Lift_data    

def limit(confidence_data, Lift_data, minConfidence = 0.5):
    limit_data = []
    for k in confidence_data.keys():
        data = []
        if confidence_data[k] >= minConfidence:
            data.append(k)
            data.append(confidence_data[k])
            data.append(Lift_data[k])
            limit_data.append(data)
    return limit_data
    
    
if __name__=='__main__':
    dataSet = loadDataSet()  # 获取事务集。每个元素都是列表
    #print(createC1(dataSet))  # 获取候选1项集。每个元素都是集合
    #D = list(map(set, dataSet))  # 转化事务集的形式，每个元素都转化为集合。
    #L1, suppDat = scanD(D, C1, 0.5)
    #print(L1,suppDat)

    L, suppData = apriori(dataSet,minSupport=0.2)
    #print(L,suppData)
    print(L[1])
    DataList, Datanum = data_deal(L,suppData)
    #print(DataList, Datanum)
    confidence_data = confidence(DataList, Datanum, suppData)
    #print(confidence_data)
    Lift_data = Lift(DataList, confidence_data, Datanum, suppData)
    #print(Lift_data)    
    limit_data = limit(confidence_data, Lift_data, minConfidence = 0.5)
    print('\n')
    for i in limit_data:
        print(i)
    draw_seaborn(suppData,len(L[0]))

​