20200503
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径5->4->11->2。
class Solution {
public:
bool hasPathSum(TreeNode* root, int sum) {
if(!root) return false;
sum = sum - root->val;
if(!root->left && !root->right && sum == 0) return true;
return hasPathSum(root->left,sum) || hasPathSum(root->right,sum);
}
};
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。
在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入: 5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> ans(numRows);
if(numRows == 0) return ans;
for(int i = 0; i < numRows; ++ i )
{
for(int j = 0; j <= i; ++ j)
{
if(j == 0 || j == i)
ans[i].push_back(1);
else
ans[i].push_back(ans[i-1][j-1] + ans[i-1][j]);
}
}
return ans;
}
};
20200504
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。

在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入: 3
输出: [1,3,3,1]
class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<vector<int>> ans(rowIndex+1);
for(int i = 0; i <= rowIndex; ++ i )
{
for(int j = 0; j <= i; ++ j)
{
if(j == 0 || j == i)
ans[i].push_back(1);
else
ans[i].push_back(ans[i-1][j-1] + ans[i-1][j]);
}
}
return ans[rowIndex];
}
};
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票一次),设计一个算法来计算你所能获取的最大利润。
注意:你不能在买入股票前卖出股票。
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int max_val = 0;
int min_val = INT_MAX;
for(int i = 0;i<prices.size();++i)
{
min_val = min(min_val,prices[i]);
max_val = max(max_val,prices[i]-min_val);
}
return max_val;
}
};
20200505
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int profit = 0;
for(int i=0;i < prices.size()-1;++i)
profit += max(prices[i+1]-prices[i],0);
return profit;
}
};
给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写。
说明:本题中,我们将空字符串定义为有效的回文串。
示例 1:
输入: "A man, a plan, a canal: Panama"
输出: true
示例 2:
输入: "race a car"
输出: false
class Solution {
public:
bool isPalindrome(string s) {
if(s.size()<=1) return true;
int i = 0,j=s.size()-1;
while(i<j)
{
while(i<j && !isalnum(s[i]))
i++;
while(i<j && !isalnum(s[j]))
j--;
if(tolower(s[i++])!=tolower(s[j--]))
return false;
}
return true;
}
};
20200506
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1]
输出: 1
示例 2:
输入: [4,1,2,1,2]
输出: 4
一个数和 0 做 XOR 运算等于本身: a⊕0 = a
一个数和其本身做 XOR 运算等于 0: a⊕a = 0
XOR 运算满足交换律和结合律: a⊕b⊕a = (a⊕a)⊕b = 0⊕b = b
class Solution {
public:
int singleNumber(vector<int>& nums) {
int res = 0;
for(int i = 0;i < nums.size();++i)
res ^= nums[i];
return res;
}
};
20200507
给定一个链表,判断链表中是否有环。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
示例 1:
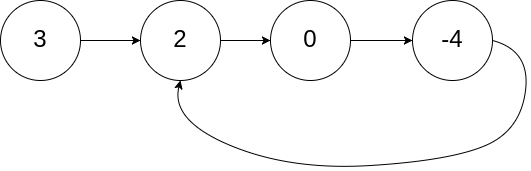
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
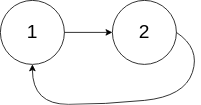
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:false
解释:链表中没有环。

/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
bool hasCycle(ListNode *head) {
ListNode* faster{ head };
ListNode* lower{ head };
if(!head) return false;
while(faster!=NULL && faster->next!=NULL)
{
faster = faster->next->next;
lower = lower->next;
if(faster == lower)
return true;
}
return false;
}
};
20200509
编写一个程序,找到两个单链表相交的起始节点。
如下面的两个链表:
在节点 c1 开始相交。
示例 1:
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Reference of the node with value = 8
输入解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Reference of the node with value = 2
输入解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
输入解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
解释:这两个链表不相交,因此返回 null。
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* A = headA;
while(A)
{
ListNode* B = headB;
while(B)
{
if(A == B)
return A;
B = B->next;
}
A = A->next;
}
return NULL;
}
};
20200511
给定一个已按照升序排列 的有序数组,找到两个数使得它们相加之和等于目标数。
函数应该返回这两个下标值 index1 和 index2,其中 index1 必须小于 index2。
说明:
返回的下标值(index1 和 index2)不是从零开始的。
你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。
示例:
输入: numbers = [2, 7, 11, 15], target = 9
输出: [1,2]
解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
int i = 0;
int j = numbers.size() - 1;
while(i < j)
{
int sum = numbers[i] + numbers[j];
if(sum < target)
i++;
else if(sum > target)
j--;
else
return vector<int>{i+1,j+1};
}
return vector<int>{-1,-1};
}
};
给定一个正整数,返回它在 Excel 表中相对应的列名称。
例如,
1 -> A
2 -> B
3 -> C
...
26 -> Z
27 -> AA
28 -> AB
...示例 1:
输入: 1
输出: "A"
示例 2:
输入: 28
输出: "AB"
示例 3:
输入: 701
输出: "ZY"
class Solution {
public:
string convertToTitle(int n) {
string ans = "";
while(n > 0)
{
n-=1;
ans.push_back('A' + (n%26));
n /= 26;
}
reverse(ans.begin(),ans.end());
return ans;
}
};
